Lijinrui299792458

不做沉底的木做举重若轻的船。

SAM 后缀自动机

发表于 更新于

SAM

如果在一个 $DAG$ 上表示一个字符串的所有子串，朴素的想法是将其所有后缀加入 $Trie$ 中，然而这样节点数是 $O(n^2)$ 的。可以发现，图中节点有很多可以合并之处。

首先是后缀本身。如果先不考虑后缀的公共前缀的存在，那么根本没有必要对每一个后缀都重新存储，可以直接用一条链表示原串，再从根指向各个节点，这样就合并了各后缀，因为只要跳过了开头的一段就可以得到一个后缀。这相当于是 $Trie$ 是菊花图时，把那些后缀拉过来，强行与最长的后缀（即原串）合并，保留那些与根相连的边。图中原串为 abc。

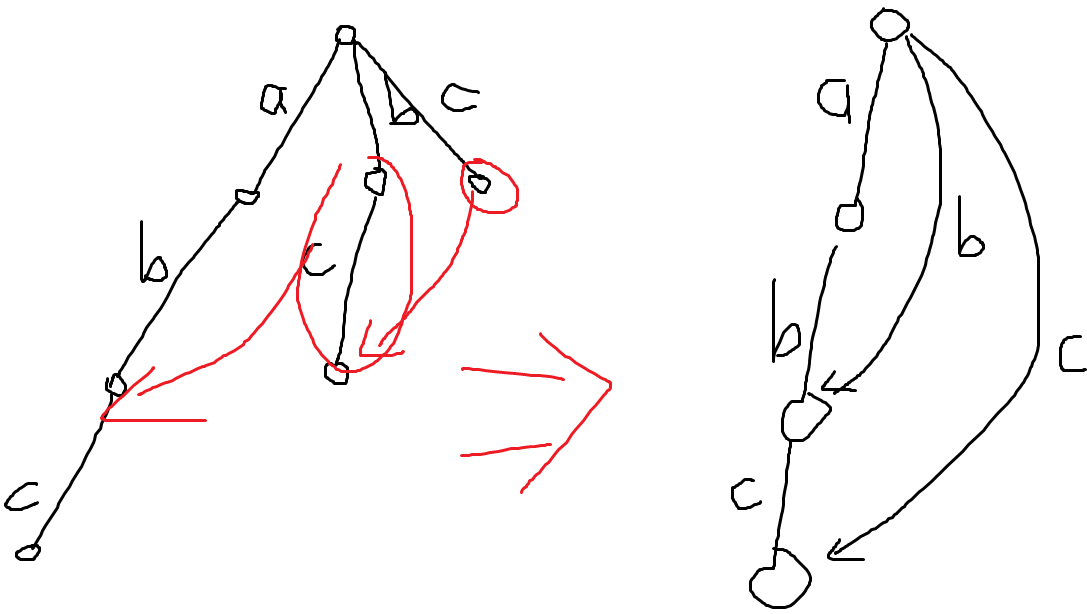
然而后缀可能存在公共的前缀，这使得 Trie 不是菊花图。这样按之前的做法，可能有一个子串出现多次。这不利于解决问题，不是我们想要的。因此 SAM 的一个限定条件是每一个子串都恰好出现一次。

考虑之前做法的本质。由于新加入一个字符 c 时该字符从未出现过，因此增加的子串为所有原有后缀加上 c 和 c 本身，即新的后缀。但如果 c 之前已经出现过，就会出现某些后缀之前出现过，就不能这样加边了。

现在假设我们建好了前 $n$ 个字符的 SAM，现在又加入了一个字符 c。首先一定会与之前的末尾字符连边，这样就有了整个串这个子串。此时新增添的子串一定是原有的能到达的后缀（即，这些后缀是在 SAM 中以到达末尾节点得到的子串，这个后缀除了在后缀的位置上外没有另外出现过）加上了 c，不可能在 SAM 中出现过，否则去掉这个字符一定也出现过。考虑那些之前出现过，但加上 c 后首次出现的后缀。

如果加入之后较大的后缀出现过，较小的后缀就一定也出现过了。因此从大到小考虑这些后缀（此处为原串后缀）。如果某个后缀对应的节点没有 c 的边就连边，否则就停止这一过程。

那么如何考察这些后缀呢？

由于每个子串至多对应一个节点，因此可以在每一个节点存储一个指向上一个子串节点的指针，其指向的节点所表示的子串为与当前节点子串由不同节点表示的后缀中最长的一个，而更短的后缀将递归得到。

现在考虑不同子串由同一个子串表示的问题。如一开始的图，"c"，"bc"，"abc" 都由同一个节点表示。但这其实不是问题，而是我们优化的结果。如果两个子串所有出现位置的右端点相同，那么这两个子串的处理不会有区别。而也只有这样的两个子串才会由同一个节点表示。贯彻落实这样的优化精神，我们称一个串 $s$ 所有出现位置的右端点组成的集合为，$\texttt{endpos}(s)$，$\texttt{endpos}(s)$ 相同的子串由同意节点表示。

$\texttt{endpos}$

关于 $\texttt{endpos}$，我们不加证明地给出结论（其实证明很简单）：

  1. 若 $\texttt{endpos}(s)=\texttt{endpos}(t),\text{len}(s)\le \text{len}(t)$，则 $s$ 是 $t$ 的后缀。
  2. 对于 $s,t,\text{len}(s)\le \text{len}(t)$，有 $\texttt{endpos}(s)\in\texttt{endpos}(t)$ 或 $\texttt{endpos}(s)\cap\texttt{endpos}(t)=\emptyset$。
  3. $\texttt{endpos}$ 相同的子串组成一个 $\texttt{endpos}$ 等价类。一个等价类中的子串为一个串的连续的一些后缀。
  4. $\texttt{endpos}$ 等价类的数量为 $O(n)$。

通过 $\texttt{endpos}$，我们将建立 $\texttt{Parent Tree}$。

$\texttt{Parent Tree}$

在一个子串的开头添加字符。一开始可能一直在原等价类内，如果每一个节点表示一个 $\texttt{endpos}$ 等价类，那么此时还一直在同一个节点上。但某一时刻节点发生变化，令新的节点是原节点的儿子。容易发现，这样建立的 $\texttt{Parent Tree}$ 上，儿子节点的 $\texttt{endpos}$ 是其父亲节点的 $\texttt{endpos}$ 的不交子集。

事实上，之前所说“与当前节点子串由不同节点表示的后缀中最长的一个”，就是在 $\texttt{Parent Tree}$ 上不断寻找父亲。

构造

回到 SAM 的构造。

加入一个字符 c，创建点 $o$，首先连之前结尾 lst 的边。接下来跳父亲直到有 c 的连边。

如果没有父亲有边，那么遍历结束，新节点父亲为 1。

如果遇到一个祖先有边，会发现一个问题。

有可能原本 $\texttt{endpos}$ 相同的子串，在加入c 后 $\texttt{endpos}$ 不同了。比如 abc，加入 c，c 的 $\texttt{endpos}$ 不同了。

先考虑这种情况没有发生：我们只需要令 $\text{fa}(o)$ 等于这个祖先节点的 c 边所通向的节点即可。

下面考虑这种情况发生。

如何判断这种情况的发生？为了方便，记所寻到的祖先节点为 $x$，$x$ 的 c 边通向 $y$。

如果在这种情况发生，一定是 $y$ 所表示的一些子串是加入之后的后缀（称“合法”），一些子串不是（非法）。这些合法子串的长度都与 $x$ 以及其通向 $y$ 的祖先所表示的子串得长度 $+1$ 一一对应，而非法的子串就一定没有一个这样的子串与之对应。由 $\texttt{endpos}$ 的性质可知非法子串一定是最长的一些子串。因此我们只要知道是否（$\text{ml}(x)$ 表示 $x$ 的等价类中最长子串的长度） $\text{ml}(x)+1=\text{ml}(y)$ 即可。因此在每个节点维护 $\text{ml}$。

现在加入之后，$y$ 点有两个等价类。因此新建一个节点 $t$，把那些 $\texttt{endpos}$ 增加了的拿出来（这些是那些合法子串，他们作为新串后缀出现了一次）。

容易知道，$\text{ml}(t)=\text{ml}(x)+1,\text{fa}(t)=\text{fa}(y),\text{fa}(y)=t,\text{fa}(o)=t$。

考虑边。首先考虑出边，虽然 $t$ 和 $y$ 的 $\texttt{endpos}$ 不同，但因为这两个节点的子串的 $\texttt{endpos}$ 差异只在原串的结尾处而这里不可能再向后拓展一个字符，在结尾加一个字符后肯定在一个等价类中，因此 $t$ 的出边只需继承 $y$ 即可。接下来考虑入边。发现 $x$ 的串为 $\texttt{endpos}$ 原非空而增加的最大的串，此时应该更改 $x$ 的串的后缀，因此跳 $x$ 的父亲。对于边 c 指向 $y$ 的点，改为让它指向 $t$。

如果遇到了一个节点的边 c 不指向 $y$，那么它一定指向 $y$ 的祖先，而 $\text{fa}(y)=t$，因此之后再也不会出现这种情况了。（相当于出了 $t$ 的等价类就不用管了，因为更短的后缀，它的儿子节点已经处理过了，那么它也就跟着把 $\texttt{endpos}$ 更新了，因此只需把原来 $y$ 里的移到 $t$ 里去就行了）

模版题 & 代码实现

题目描述

P3804 【模板】后缀自动机 (SAM)

做法

即求 $\max_{x}(\text{sizeof}(\texttt{endpos}(x))\text{ml}(x))$。

在 $\texttt{Parent Tree}$ 上 DFS，显然有 $\texttt{endpos}$ 等于所有儿子 $\texttt{endpos}$ 和本身如果是前缀前缀的结束位置之并。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;

struct SAM
{
	int ch[26],fa,ml;bool fl;
}sam[2000000];int tot,lst;

void buil(int c)
{
	int x=lst;lst=++tot;sam[lst].fl=1;sam[lst].ml=sam[x].ml+1;
	while((x)&&(!sam[x].ch[c]))sam[x].ch[c]=lst,x=sam[x].fa;
	if(!x)//case 1
	{
		sam[lst].fa=1;
		return;
	}
	int y=sam[x].ch[c];
	if(sam[x].ml+1==sam[y].ml)//case 2
	{
		sam[lst].fa=y;
		return;
	}
	++tot;//case 3
	sam[tot]=sam[y],sam[tot].fl=0;sam[tot].ml=sam[x].ml+1;sam[y].fa=sam[lst].fa=tot;
	while((x)&&(sam[x].ch[c]==y))sam[x].ch[c]=tot,x=sam[x].fa;
}

long long ans=0;int nxt[3000000],to[3000000],cnt,h[2000000];
void ad(int u,int v)
{
	to[++cnt]=v;
	nxt[cnt]=h[u];
	h[u]=cnt;
}
int dfs(int x)
{
	int ret=(sam[x].fl);
	for(int i=h[x];i;i=nxt[i])
	ret+=dfs(to[i]);
	if(ret>1)ans=max(ans,1LL*ret*sam[x].ml);
	return ret;
}

int main(){
	char c;tot=lst=1;
	while((c=getchar())>='a'&&c<='z')buil(c-'a');
	for(int i=2;i<=tot;i++)ad(sam[i].fa,i);
	dfs(1);
	printf("%lld",ans);
}

复杂度

点

由 $\texttt{endpos}$ 的数量可知为 $O(n)$。

边

首先建一个生成树，边数 $O(n)$。

如果在自动机上跑遍所有子串必然遍历到所有边，但我们不需要这样做。考虑到所有的子串都一定是某个后缀的前缀，因此只需跑所有的后缀。

我们从 lst 出发，逆向跑回 1 节点。

而在跑每一个后缀的时候，如果发现走不通，就加一条应该走的边。注意到此时这条边所通向节点一定可以通向 1 节点（有树做基础），并且这样走由于经过了刚才新添加的边，因此一定产生新的后缀。由此可以发现，每加一条边，至少可以多一个后缀。因此边也是 $O(n)$ 的。

时间

注意到其中两个 while 是时间复杂度不确定的原因。

对于：

1
while((x)&&(!sam[x].ch[c]))sam[x].ch[c]=lst,x=sam[x].fa;

事实上是加边，因此是 $O(n)$ 的。

而：

1
while((x)&&(sam[x].ch[c]==y))sam[x].ch[c]=tot,x=sam[x].fa;//case 3

我们知道这句是将 $\texttt{endpos}(y)$ 中的串移到 $\texttt{endpos}(t)$ 中。

如果这次 case 3 和上一次已经相互独立（指新建节点中的后缀的左端点的范围不交），那么转移的串数一定不多于这一段范围大小，因此 $O(n)$。

否则，考虑上一次 case 3，考虑这两次修改的子串的共同范围：

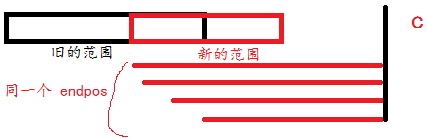
可以发现，重复范围内开头的后缀属于同一个 $\texttt{endpos}$（当时新建节点的 $\texttt{endpos}$ 通过特定路径到达的节点，因为此间未发生一个 $\texttt{endpos}$ 分裂），因此平均还是 $O(n)$ 的。

学习资料

The smallest automation recognizing the subwords of a text - ScienceDirect

史上最通俗的后缀自动机详解 - KesdiaelKen 的博客