一些关于 wqs 的例题和拓展。如果题目有贪心等做法也会给出。
每次给白边的边权 +c 二分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #include<bits/stdc++.h>
using namespace std;
void read(int &x)
{
x=0;char c;
while((c=getchar())<'0'||c>'9');
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
}
struct edge
{
int s,t,c,_c,col;
void ad(int cc){if(!col)_c=c+cc;}
}e[100005];
bool operator < (edge e1,edge e2){return ((e1._c==e2._c)?(e1.col<e2.col):(e1._c<e2._c));}
int fa[100005];
int root(int u)
{
if(!fa[u])return u;
return (fa[u]=root(fa[u]));
}
void merge(int u,int v){fa[root(u)]=root(v);}
int n,m,nd;
int chk(int x)
{
for(int i=1;i<=m;i++)e[i].ad(x);
sort(e+1,e+1+m);
memset(fa,0,sizeof(fa));
int l=n-1,i=1,ret=0;
while(l)
{
while(root(e[i].s)==root(e[i].t))i++;
ret+=e[i].col^1;
merge(e[i].s,e[i].t);++i,--l;
}
return ret;
}
int binary(int l,int r,int val)
{
int mid,tmp;
while(l<=r)
{
mid=l+r>>1;
tmp=chk(mid);
if(tmp<nd)r=mid-1;
else l=mid+1;
}
return r;
}
int main()
{
read(n),read(m),read(nd);
for(int i=1;i<=m;i++)read(e[i].s),read(e[i].t),e[i].s++,e[i].t++,read(e[i].c),read(e[i].col),e[i]._c=e[i].c;
int cc=binary(-100,100,nd);
for(int i=1;i<=m;i++)e[i].ad(cc);
sort(e+1,e+1+m);
memset(fa,0,sizeof(fa));
int l=n-1,i=1,ans=0;
while(l)
{
while(root(e[i].s)==root(e[i].t))i++;
ans+=e[i]._c;
merge(e[i].s,e[i].t);++i,--l;
}
ans-=cc*nd;
printf("%d",ans);
return 0;
}
|
法 1:wqs
每次给与 s 相连的边的边权 +c 二分。判无解:求的的偏移量不在合法范围内。
法 2:贪心
约定:
- s 边:与 s 相连的边
- i 方案:选择 i 条 s 边的一种生成树方案
- i 答案:i 方案中的最优情况
- 点权:与其相连所有 s 边的最小边权
- 其他约定以括号形式给出
每一个 i 答案都是有 i 条 s 边,断开他们得到 i 棵树的森林。那么与 s 相连的点一定是所在树中点权最小的点。
我们想要证明,i 答案一定由 i-1 答案增加一条 s 边得到。
假设我们已得到 i-1 答案,却发现 i 答案不能从 i-1 答案通过增加一条 s 边,即连通一个点与 s 点,并删去原有的一条树边得到。
那么这一定是有一个 i-1 方案此次所连接的 $u$ 点和断开 $v$ 点造成的贡献比较大,而在 i 答案中却不能这样做。
我们一定是选择一个点 $x$,加上它的点权,减去它到他所在的树的树根 $\text{root}(x)$ 的路径 $\text{path}(x)$ 上一条边的边权。这两个符号的下标表示对应于 i 方案 / 答案。
如果 $u$ 与 $v$ 在同一树中,那么在 i 答案中新删去的边在 i-1 答案中一定在 $\text{path}{i-1}(u)$ 或 $\text{path}{i-1}(v)$ 上,那么一定有方法在 i-1 答案上产生更优的解。如果他们在不同树中而满足同样地条件,同理也可以更优。
否则,应断开的那条边 $x$ 一定已经断开,如图:
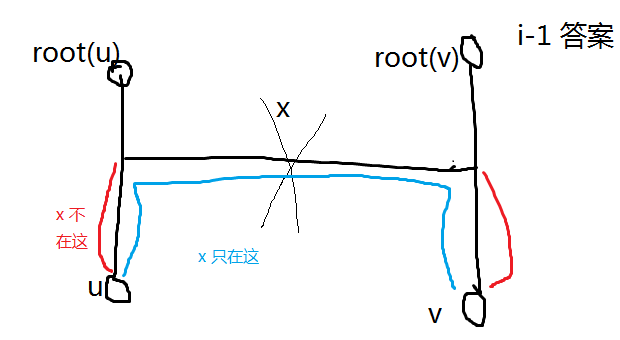
可以想到调整断开的顺序:如果调换 $\texttt{split}(\alpha,\text{root}(\alpha),y)$ (通过断开 $y$ 断开两点)和 $\texttt{split}(\beta,\text{root}(\beta),z)$,如果相互独立答案肯定不变。如果 $\text{root}(\beta)=\alpha$,如果断开此边能正常断开答案仍不边;否则变成 $\texttt{split}(\alpha,\text{root}(\alpha),z)$ 然后 $\texttt{split}(\beta,\text{root}(\beta),y)$,答案不变。也就是说,答案只与我们选择了那些点,又断开了哪些边有关,与我们断开的顺序无关,只要他是合法的。而上面所证,即我们调换点的顺序,也总可以找到合法的方式。
那么贪心的正确性就很容易证明了。
我们可以从点所删除的边出发,也可以从边所对应的点出发。
如果从点删边出发,我们需要求
主要在于输出方案。
我们知道,如果我们所求出的偏移量的最小生成树不是恰好符合要求的,一定是因为有一些 1 出发的边和非 1 出发的边的边权相等,我们优先选择了 1 出发的边,导致选的太多了。那么我们再二分我们优先选择的程度:选择了 kth 条 1 出发的边后就优先选择非 1 出发的边。具体实现看代码。
Code
排序和存储方式
桶排,这样一只 $\log$,而且更方便 krus 中的优先程度修改。
krus
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| int krus(int mov,int kth)
{
memcpy(cur,hd0,sizeof(hd0));
memset(fa,0,sizeof(fa));
int cntk=0,cntb=n-1;
if(mov<0)
{
for(int i=0;i<-mov&&cntb;i++)for(int j=hd0[i];j;j=e[j].nxt)if(merge(e[j].s,e[j].t))++cntk;
for(int i=0,ii=-mov;ii<=100000&&cntb;i++,ii++)
{
for(int &j=cur[ii];j&&kth>cntk&&cntb;j=e[j].nxt)if(merge(e[j].s,e[j].t))++cntk,--cntb;
for(int j=hd[i];j&&cntb;j=e[j].nxt)cntb-=merge(e[j].s,e[j].t);
for(int j=cur[ii];j&&cntb;j=e[j].nxt)if(merge(e[j].s,e[j].t))++cntk,--cntb;
}
for(int i=100001+mov;i<=100000&&cntb;i++)for(int j=hd[i];j&&cntb;j=e[j].nxt)cntb-=merge(e[j].s,e[j].t);
return cntk;
}
for(int i=0;i<mov&&cntb;i++)for(int j=hd[i];j;j=e[j].nxt)cntb-=merge(e[j].s,e[j].t);
for(int i=mov,ii=0;i<=100000&&cntb;i++,ii++)
{
for(int &j=cur[ii];j&&kth>cntk&&cntb;j=e[j].nxt)if(merge(e[j].s,e[j].t))++cntk,--cntb;
for(int j=hd[i];j&&cntb;j=e[j].nxt)cntb-=merge(e[j].s,e[j].t);
for(int j=cur[ii];j&&cntb;j=e[j].nxt)if(merge(e[j].s,e[j].t))++cntk,--cntb;
}
for(int i=100001-mov;i<=100000&&cntb;i++)for(int j=hd0[i];j;j=e[j].nxt)if(merge(e[j].s,e[j].t))++cntk;
if(cntb)return 100010;
return cntk;
}
|
二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int chk1(int x){return krus(x,100000);}
int chk2(int x){return -krus(mov,x);}
int binary(int l,int r,int v,int (&chk)(int x))
{
int mid,tmp;
while(l<=r)
{
mid=l+r>>1;
tmp=chk(mid);
if(tmp==v)return mid;
if(tmp>v)l=mid+1;
else r=mid-1;
}
return r;
}
|
主函数:
1
2
| if(so1==m)mov=0;else mov=binary(-100010,100010,k,chk1);
int kth=binary(0,so1,-k,chk2)+1,
|
