SAM

如果在一个 $DAG$ 上表示一个字符串的所有子串，朴素的想法是将其所有后缀加入 $Trie$ 中，然而这样节点数是 $O(n^2)$ 的。可以发现，图中节点有很多可以合并之处。

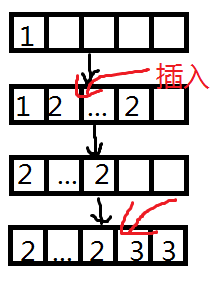
首先是后缀本身。如果先不考虑后缀的公共前缀的存在，那么根本没有必要对每一个后缀都重新存储，可以直接用一条链表示原串，再从根指向各个节点，这样就合并了各后缀，因为只要跳过了开头的一段就可以得到一个后缀。这相当于是 $Trie$ 是菊花图时，把那些后缀拉过来，强行与最长的后缀（即原串）合并，保留那些与根相连的边。图中原串为 abc。

然而后缀可能存在公共的前缀，这使得 Trie 不是菊花图。这样按之前的做法，可能有一个子串出现多次。这不利于解决问题，不是我们想要的。因此 SAM 的一个限定条件是每一个子串都恰好出现一次。

考虑之前做法的本质。由于新加入一个字符 c 时该字符从未出现过，因此增加的子串为所有原有后缀加上 c 和 c 本身，即新的后缀。但如果 c 之前已经出现过，就会出现某些后缀之前出现过，就不能这样加边了。

现在假设我们建好了前 $n$ 个字符的 SAM，现在又加入了一个字符 c。首先一定会与之前的末尾字符连边，这样就有了整个串这个子串。此时新增添的子串一定是原有的能到达的后缀（即，这些后缀是在 SAM 中以到达末尾节点得到的子串，这个后缀除了在后缀的位置上外没有另外出现过）加上了 c，不可能在 SAM 中出现过，否则去掉这个字符一定也出现过。考虑那些之前出现过，但加上 c 后首次出现的后缀。

如果加入之后较大的后缀出现过，较小的后缀就一定也出现过了。因此从大到小考虑这些后缀（此处为原串后缀）。如果某个后缀对应的节点没有 c 的边就连边，否则就停止这一过程。

那么如何考察这些后缀呢？

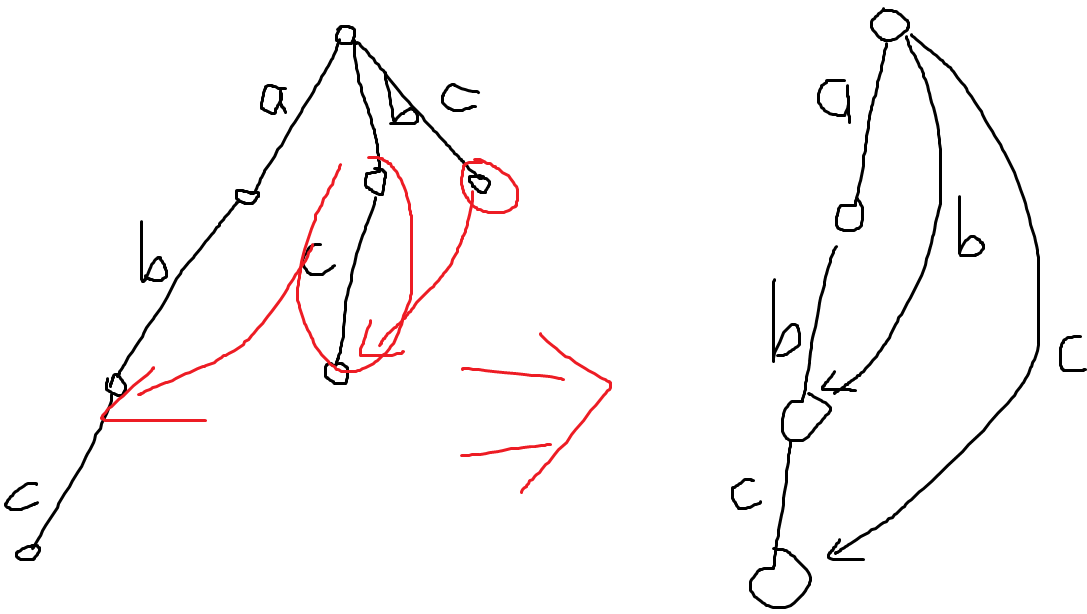
由于每个子串至多对应一个节点，因此可以在每一个节点存储一个指向上一个子串节点的指针，其指向的节点所表示的子串为与当前节点子串由不同节点表示的后缀中最长的一个，而更短的后缀将递归得到。

题目描述

$1<n,m\le 10^3,m\le t\le 10^9$

思路

考虑序列的第一位，如果该位确定，那么问题转化为求 $n-1$ 位问题。但这 $n-1$ 位中第一位可能会与整个序列第一位发生合并。我们更希望出现的情况是第一位确定。故设 $p_{i,j}$ 为限制长度为 $i$，首位出现过 $j$ 的概率，即当该序列之前是 $j$ 时发生合并的概率，而在出现了 $j$ 前提下首位保持不变的概率为 $q_{i,j}$。如果第一位保持为 $j$，相当于有后 $i-1$ 位的首位未出现过 $j$，即 $q_{i,j}=1-p_{i-1,j}$。（$j=t$ 时特判，下文不再重复）

当第一位出现了 $j$ 时，可能有两种情况：

1. 两个 $j-1$ 合并，即 $p_{i,j-1}\cdot p_{i-1,j-1}$
2. 直接加入 $j$，概率 $\frac{1}{m}$

在第一位保持为 $j$ 的情况下考虑求解：设以此为前提，期望和为 $g_{i,j}$，则 $ans_i=\sum_{j=1}^{lim}p_{i,j}q_{i,j}g_{i,j}$。设 $f_{i,j}$ 为第一位产生 $j$ 前提下期望和，有：
$$
g_{i,j}=j+\frac{ans_{i-1}-p_{i-1,j}f_{i-1,j}}{q_{i,j}}
$$
考虑求 $f$。讨论 $j$ 是否保持不变，得：
$$
f_{i,j}=q_{i,j}g_{i,j}+(1-q_{i,j})f_{i,j+1}
$$
显然 $lim=\min(n+m-1,t)$，时间复杂度 $O(nm\log(10^9+7))$。但如果不求 $g_{i,j}$，而是求 $q_{i,j}g_{i,j}$，则可以做到 $O(nm)$。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

#include<bits/stdc++.h>

using namespace std;

const int mod=1e9+7;
int p[1001][2001],q[1001][2001],g[2001],f[2001],ans;
int m,n,t,lim;

int pow(int x,int y)
{
	int ret=1;
	while(y)
	{
		if(y&1)ret=1LL*ret*x%mod;
		x=1LL*x*x%mod;
		y>>=1;
	}
	return ret;
}

int main()
{
	freopen("sequence.in","r",stdin);
    freopen("sequence.out","w",stdout);
    scanf("%d%d%d",&n,&m,&t);
	lim=min(n+m-1,t);
	int m_1=pow(m,mod-2),an;
	for(int i=1;i<=n;i++)for(int j=1;j<=lim;j++)p[i][j]=(1LL*p[i][j-1]*p[i-1][j-1]+1LL*(j<=m)*m_1)%mod,q[i][j]=(1-(j<lim)*p[i-1][j]+mod)%mod;
	for(int i=1;i<=lim;i++)g[i]=f[i]=i,ans=(1LL*p[1][i]*q[1][i]%mod*i+ans)%mod;
	for(int i=2;i<=n;i++)
	{
		an=ans;ans=0;
		for(int j=1;j<=lim;j++)
		{
			int _=an-(j<lim?1LL*p[i-1][j]*f[j]%mod:0)+mod;
			g[j]=(1LL*q[i][j]*j+_)%mod;ans=(1LL*p[i][j]*g[j]%mod+ans)%mod;
		}
		for(int j=lim;j;j--)f[j]=(1LL*g[j]%mod+1LL*(1-q[i][j]+mod)*f[j+1]%mod)%mod;
	}
	printf("%d\n",ans);
	return 0;
}

题目描述

$n\le 3000,m\le 300$

思路

肯定是要算贡献的。

考察一个礼物的贡献，用 $g_{i,j}$ 表示其贡献，即：第 $i$ 种礼物有 $j$ 个，期望被拿走的个数。

考虑从 $g_{i,j}$ 转移到 $g_{i,j+1}$，发现这取决于喜欢这种礼物的人数。考虑有 $k$ 个人喜欢这种礼物的概率，用 $h_{i,j,k}$ 表示前 $j$ 个人中有 $k$ 个人喜欢 $i$ 礼物的概率。此时 $g_{i,j}=\sum_{x=0}^{n}\min (x,j)h_{i,n,x}$，进而 $g_{i,j}-g_{i,j-1}=\sum_{x=j}^nh_{i,n,x}$。

进而买 $j$ 件前 $i$ 种礼物的期望值为：$f_{i,j}=\max(f_{i-1,j-x}+g_{i,x})$。发现 $g$ 的差分不增，故可以转换为贪心，每次寻找 $g$ 增量最大的种类。

此时瓶颈在于求 $h$。
$$
h_{i,j,k}=(1-p)h_{i,j-1,k}+ph_{i,j-1,k-1}
$$
发现我们每次用一个 $\Delta g$ 更新后，只需知道 $\sum_{x=j}^nh_{i,n,x}$，而之前一定已经求过 $\sum_{x=j-1}^nh_{i,n,x}$，故只需求 $h_{i,n,j-1}$，而此前必求过 $h_{i,n,j-2}$，故可以递推，并不需要知道全部 $h$。

复杂度是对的。

题目描述

CF346D Robot Control

思路

可以想到，对于每一个节点，$dp[x]$ 表示其走到终点所需的最少指令数。考虑状态的转移：如果下指令，则 $dp[i]$ 为其出边所通向的点中的最小值加一。若不下指令则取最大值，两种情况取最小值。即，
$$
dp[x]=\min\{\min_{x\to y}\{dp[y]\}+1,\max_{x\to y}\{dp[y]\}\}
$$
你能解决问题的一部分吗？

可以发现下指令的部分类似于一个边权为 $1$ 的最短路，尝试用 $BFS$ 解决。我们先对 $BFS$ 的过程进行一下概括，$BFS$ 时队列中的元素如下：

可以发现，队列中元素（指 $dp$ 值）总是连续的 $n$ 和 $n+1$，且不降。在反图上 $BFS$，每次取队首元素进行更新，从队尾插入。

再考虑不钦定前进方向的情况。（称“第二类”）

枚举 $x$ 的所有出边（在原图上），如果发现指向的点的 $dp$ 值的最大值小于 $dp[x]$，则更新，同时在队首插入 $x$ 以保证单调性在 $x$ 出队时，如果 $x$ 能被第二类更新，显然它应该先被更新再更新别的点，这样不会在非最优值上浪费时间，而此时第二类更新 $x$ 的点一定已经被更新，因此 $x$ 一出队就对其更新，时间复杂度正确，而正确性显然。

Code

置换群

1. 置换：置换是一个集合映至自身的双射。$(a_1,a_2,\cdots,a_n)$ 表示将原数列的第 $a_i$ 个数在此置换作用下变到第 $i$ 个位置。

2. 对于状态 $s$ 和置换 $f$，记 $f*s$ 为将 $f$ 作用于 $s$ 所得到的状态。

3. 定义置换的乘法：$f\cdot g$ 表示显作用 $g$ 再作用 $f$。

4. 置换群：有限集合上的一些置换组成的集合在置换的乘法下组成的群。

5. 等价类：若状态组成的集合 $X$ 中的元素经过置换群 $G$ 中的置换作用后可以变成相同的状态，则这些状态属于一个等价类。等价类组成的集合记为 $X/G$。

6. 循环：如果一个置换 $f=(a_1,a_2,\cdots,a_n)$，存在 $k$ 个元素使得 $a_{x_1}=x_2,a_{x_2}=x_3,\cdots,a_{x_k}=x_1$，则称 $x_1,x_2,\cdots,x_k$ 为一个长度为 $k$ 的循环。一个置换可以被拆分为一些不相交的循环，如：
   $$
   (6,5,7,4,1,2,3)=(1,6,2,5)\circ(3,7)\circ(4)
   $$

7. 轨道与稳定子：
   $$
   X^{\tau}={s|s\in X,\tau*s=s}
   $$

   $$
   G(s)={\tau*s|\tau\in G}
   $$

   $G(s)$ 称为 $s$ 的轨道。
   $$
   G^s={\tau|\tau*s=s}
   $$
   $G^s$ 称为 $s$ 的稳定子。

Burnside 引理

$$
\left|X/G\right|=\frac{\sum_{\tau\in G}\left|X^\tau\right|}{\left|G\right|}
$$

证明：
$$
\sum_{\tau\in G}\left|X^\tau\right|=\sum_{\tau\in G}\sum_{s\in X}[\tau*s=s]
$$

$$
=\sum_{s\in X}\sum_{\tau\in G}[\tau*s=s]=\sum_{s\in X}\left|G^s\right|
$$

注意到，$s$ 所在的等价类的大小（记为 $|L_s|$）为 $\tau*s$ 的所有可能结果数。

联想拉格朗日定理，可以猜想：$\left|G^s\right|=\frac{|G|}{|L_s|}$。

首先易证，$G^{s}$ 是 $G$ 的子群。

若 $\alpha,\beta\in G$，$\alpha*s=\beta*s$，

欧拉定理的推广

欧拉定理要求 $\gcd(a,m)=1$，因此在 $a,m$ 不互质时无法直接使用。对于 $a,m$，若 $gcd(m,a)\ne 1$ 且 $x>\varphi(m)$，有
$$
a^x\equiv a^{x\mod\varphi(m)+\varphi(m)}\mod m
$$
证明：
$$
m=\prod_{i=1}^{n}p_i^{q_i},a=s\prod_{i=1}^{n}p_i^{k_i},\gcd(s,m)=1
$$

$$
即证:t\ge1,a^{t\varphi(m)}\equiv s^{t\varphi(m)}\prod_{i=1}^{n}p_i^{t\varphi(m)k_i}\equiv a^{\varphi(m)}\mod m
$$

$$
对于 k_i=0,p_i^{t\varphi(m)k_i}\equiv1\mod m
$$

$$
\varphi(m)\ge\varphi(p_i^{q_i})=p_i^{q_i-1}(p_i-1)\ge2^{q_i-1}\ge q_i
$$

$$
p_i^{b\varphi(m)}\equiv1 \mod \left(\frac{m}{p_i^{q_i}}\right),p_i^{b\varphi(m)+q_i}\equiv p_i^{q_i}\mod m
$$

$$
p_i^{(b+1)\varphi(m)}\equiv p_i^{\varphi(m)}\mod m
$$

显然，原命题成立。

例

P4139 上帝与集合的正确用法

费马小定理

若 $p$ 为质数，$a$ 不是 $p$ 的倍数，则 $a^{p-1}\equiv 1(\mod p)$

证明：

$0<t<p,ta$ 在 $\mod p$ 下互不相同，因为如果 $t\neq k,ta\equiv ka(\mod p),t\equiv k(\mod p)$

故 $a^{p-1}(p-1)!\equiv(p-1)!(\mod p),a^{p-1}\equiv 1(\mod p)$

积性函数

任意 $\gcd(m,n)=1$，有 $f(m)f(n)=f(mn)$，则 $f(x)$ 为积性函数。特殊地，若对任意 $m,n$ 都有 $f(m)f(n)=f(mn)$，则 $f(x)$ 为完全积性函数。

注：常见的积性函数：

• $\epsilon(x)=[x=1]$
• $1(n)=1$
• $id_k(n)=n^k$
• $\sigma_k(n)=\sum_{d|n}d^k$
• $\varphi(n)$：一会要说的欧拉函数
• $\mu(n)$：以后会说的莫比乌斯函数

欧拉函数

Introduction

Theory

注：在以下讨论中将不会考虑 $[ \ ]$ 和 $[2^2]$ 单独出现的乏趣情形。

可以想到将一个长的串分割为数个不相干的段。考虑段之间的情形，即考虑一个段的开头和结尾。

在此之前，对于从 $[a^{\alpha}b^{\beta}\cdots]$ 开始的序列，若
$$
[a^{\alpha}b^{\beta}\cdots]\to[(a’)^{\alpha’}(b’)^{\beta’}\cdots]
$$
显然 $\alpha’\le\lfloor\lg\alpha\rfloor+\lfloor\lg\beta\rfloor+3$，故在充分多次操作后串中不可能出现 $X^{\ge4} \ or \ X^3Y^3 \ or\ 3^3$

故，若考虑一个没有 $X^{\ge4} \ or \ X^3Y^3 \ or\ 3^3$ 的串的开头，讨论可能出现的情况：
$$
[n^m(n\ge4)\to[m^1
$$

$$
\begin{array}{l}[n^1(n\ge4)\to[1^1X^1\to[1^3\to[3^1X^{(\ne3)}\to[1^1X^1\end{array}
$$

$$
\begin{array}{l}[1^1X^{\ne1}&\to &[1^2X^1 &\to&[2^11^2&\to&[1^12^2&\to&[1^2X^{\ne2}\\
&\searrow\\
& &[1^2X^{\ne1}&\to&[2^1X^{\ne2}&\to&[1^1X^1\end{array}
$$

数列

对于数列 $a_n=pa_{n-1}+qa_{n-2}$，已知 $a_1,a_2$，求通项公式。

对于此类问题，基本的思想是在等式两边制造同构。不妨设同构的部分是 $a_n-ta_{n-1}$，则：
$$
a_n-ta_{n-1}=(p-t)(a_{n-1}-ta_{n-2})-(t^2-pt-q)a_{n-2}
$$

$$
\therefore t^2-pt-q=0
$$
$t^2-pt-q=0$ 称为数列 ${a_n}$ 的特征方程，其根称为 ${a_n}$ 的特征根。

如果方程有不等两根（不是实根也可以），那么将推出的两个式子（分别用两根推出 $a_n-ta_{n-1}$ 的通项）作差，消去 $a_n$ 项。

若方程两根相等，则 $t=\frac{p}{2},p-t=t$，最后可以整理出 $\frac{a_n}{t^n}$ 是等差数列。

微分方程

特征根法同时也是解常系数齐次线性微分方程的方法。

对于 $y’’-py’-qy=0$，设 $y’’-ry’=(p-r)(y’-ry’’)$，则 $r^2-pr-q=0$。