Introduction


Theory
注:在以下讨论中将不会考虑 $[ \ ]$ 和 $[2^2]$ 单独出现的乏趣情形。
可以想到将一个长的串分割为数个不相干的段。考虑段之间的情形,即考虑一个段的开头和结尾。
在此之前,对于从 $[a^{\alpha}b^{\beta}\cdots]$ 开始的序列,若
$$
[a^{\alpha}b^{\beta}\cdots]\to[(a’)^{\alpha’}(b’)^{\beta’}\cdots]
$$
显然 $\alpha’\le\lfloor\lg\alpha\rfloor+\lfloor\lg\beta\rfloor+3$,故在充分多次操作后串中不可能出现 $X^{\ge4} \ or \ X^3Y^3 \ or\ 3^3$
故,若考虑一个没有 $X^{\ge4} \ or \ X^3Y^3 \ or\ 3^3$ 的串的开头,讨论可能出现的情况:
$$
[n^m(n\ge4)\to[m^1
$$
$$
\begin{array}{l}[n^1(n\ge4)\to[1^1X^1\to[1^3\to[3^1X^{(\ne3)}\to[1^1X^1\end{array}
$$
$$
\begin{array}{l}[1^1X^{\ne1}&\to &[1^2X^1 &\to&[2^11^2&\to&[1^12^2&\to&[1^2X^{\ne2}\\
&\searrow\\
& &[1^2X^{\ne1}&\to&[2^1X^{\ne2}&\to&[1^1X^1\end{array}
$$
$$
\begin{array}{l}[2^1X^2\to[1^1X^{\ne1}\end{array}
$$
$$
\begin{array}{l}[2^3X^{\ne2}\to[3^12^1\end{array}
$$
$$
[2^3X^2\to[3^12^2
$$
$$
[3^1\to[1^1
$$
$$
[3^2\to[2^1
$$
除了 $[2^2$,所有的串都将进入 $[1^1X^1\to[1^3\to[3^1X^{(\ne3)}\to[1^1X^1$ 的循环。
$$
[2^21^1X^1\to[2^21^3\to[2^23^1X^{\ne3}\to[2^21^1X^1
$$
$$
[2^21^1X^{\ne1}\to[2^21^2\to[2^3
$$
$$
[2^2X^2\to[2^3
$$
$$
[2^2(\ne1,\ne2)^1\to[2^21^1
$$
另一个循环是 $[2^21^1X^1\to[2^21^3\to[2^23^1X^{\ne3}\to[2^21^1X^1$
进行下一步之前,还需要一个引理:如果一个段是 $n$ 结尾的,那么它永远是 $n$ 结尾的。
现在如果 $[LR]$ 中 $L$ 和 $R$ 是两个独立的段,那么将此串记作 $[L.R]$。表中的 $LR$ 都可记作 $L.R$。
| $L$ | $R$ |
|---|---|
| $n](n\ge4)$ | $[m(m\le3)$ |
| $2]$ | $[n^1 \ or \ [1^1X^1 \ or \ [1^3 \ or \ 3^1X^{(\ne3)}$ (循环 1) |
| $\ne2]$ | $[2^21^1X^1 \ or \ [2^21^3 \ or\ [2^23^1X^{(\ne3)} \ or \ [2^2] \ or\ [2^2n^1$ (循环 2) |
对于结尾:
$$
1^3]\to(\ne2)1^1]\to(\ne2)1^2]\to2^{\ne2}1^1]\to2^{(\ne2)}1^2]\to2^21^1]\to2^21^2]\to2^31^1]
$$
对于 $n>1:$
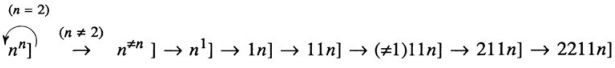

可以看到在循环中所出现的一些段:
$$
11132\to 311312\to 1321131112\to 11131221133112\to 311311222.12.32112
$$
$$
311311222\to1321132.132
$$
$$
1321132\to111312211312\to3113112221131112\to1321132.13221133112
$$
$$
13221133112\to1113222.12.32112
$$
$$
1113222\to311332\to132.12.312
$$
$$
132\to111312\to31131112\to1321133112\to11131.22.12.32112
$$
$$
12\to1112\to3112\to132112\to1113122112\to311311222112\to1321132.1322112
$$
$$
1322112\to1113222112\to3113322112\to132.123222112
$$
$$
123222112\to111213322112\to31121123222112\to132112211213322112\to111312212221121123222112\to
$$
$$
3113112211322112211213322112\to1321132122211322212221121123222112\to
$$
$$
111312211312113221133211322112211213322112\to31131122211311122113222.12.312211322212221121123222112
$$
$$
31131122211311122113222\to1321132.13221133122211332
$$
$$
13221133122211332\to1113222.12.3113.22.12.312
$$
$$
3113\to132113\to1113122113\to311311222113\to1321132.1322113
$$
$$
1322113\to1113222113\to3113322113\to132.123222113
$$
$$
123222113\to111213322113\to31121123222113\to132112211213322113\to111312212221121123222113\to
$$
$$
3113112211322112211213322113\to1321132122211322212221121123222113\to
$$
$$
111312211312113221133211322112211213322113\to31131122211311122113222.12.312211322212221121123222113
$$
$$
312211322212221121123222113\to13112221133211322112211213322113\to
$$
$$
11132.13.22.12.312211322212221121123222113
$$
$$
13\to1113\to3113
$$
$$
312211322212221121123222112\to13112221133211322112211213322112\to
$$
$$
11132.13.22.12.312211322212221121123222112
$$
$$
312\to131112\to11133112\to312.32112
$$
$$
32112\to13122112\to111311222112\to31132.1322112
$$
$$
31132\to13211312\to11131221131112\to3113112221133112\to1321132.13.22.12.32112
$$
$$
13211322211312113211\to1113122113322113111221131221\to311311222.12322211331222113112211
$$
$$
12322211331222113112211\to1112133.22.12.311322113212221
$$
$$
1112133\to3112112.3
$$
$$
3112112\to1321122112\to11131221222112\to3113112211322112\to13211321222113222112\to
$$
$$
11131221131211322113322112\to31131122211311122113222.123222112
$$
$$
3\to13
$$
$$
311322113212221\to13211322211312113211
$$
$$
11131\to311311\to13211321\to11131221131211\to311311222113111221\to1321132.1322113312211
$$
$$
1322113312211\to1113222.12.3112221
$$
$$
3112221\to132.13211
$$
$$
13211\to11131221\to3113112211\to132113212221\to111312211312113211\to311311222113111221131221
$$
$$
\to1321132.132211331222113112211
$$
$$
132211331222113112211\to1113222.12.311322113212221
$$
$$
311322113212221\to13211322211312113211
$$
整理可得 92 个基本串,即元素:
| # | Subsequence | Len | Evolves Into |
|---|---|---|---|
| 1 | 1112 | 4 | (63) |
| 2 | 1112133 | 7 | (64)(62) |
| 3 | 111213322112 | 12 | (65) |
| 4 | 111213322113 | 12 | (66) |
| 5 | 1113 | 4 | (68) |
| 6 | 11131 | 5 | (69) |
| 7 | 111311222112 | 12 | (84)(55) |
| 8 | 111312 | 6 | (70) |
| 9 | 11131221 | 8 | (71) |
| 10 | 1113122112 | 10 | (76) |
| 11 | 1113122113 | 10 | (77) |
| 12 | 11131221131112 | 14 | (82) |
| 13 | 111312211312 | 12 | (78) |
| 14 | 11131221131211 | 14 | (79) |
| 15 | 111312211312113211 | 18 | (80) |
| 16 | 111312211312113221133211322112211213322112 | 42 | (81)(29)(90) |
| 17 | 111312211312113221133211322112211213322113 | 42 | (81)(29)(91) |
| 18 | 11131221131211322113322112 | 26 | (81)(30) |
| 19 | 11131221133112 | 14 | (75)(29)(92) |
| 20 | 1113122113322113111221131221 | 28 | (75)(32) |
| 21 | 11131221222112 | 14 | (72) |
| 22 | 111312212221121123222112 | 24 | (73) |
| 23 | 111312212221121123222113 | 24 | (74) |
| 24 | 11132 | 5 | (83) |
| 25 | 1113222 | 7 | (86) |
| 26 | 1113222112 | 10 | (87) |
| 27 | 1113222113 | 10 | (88) |
| 28 | 11133112 | 8 | (89)(92) |
| 29 | 12 | 2 | (1) |
| 30 | 123222112 | 9 | (3) |
| 31 | 123222113 | 9 | (4) |
| 32 | 12322211331222113112211 | 23 | (2)(61)(29)(85) |
| 33 | 13 | 2 | (5) |
| 34 | 131112 | 6 | (28) |
| 35 | 13112221133211322112211213322112 | 32 | (24)(33)(61)(29)(90) |
| 36 | 13112221133211322112211213322113 | 32 | (24)(33)(61)(29)(91) |
| 37 | 13122112 | 8 | (7) |
| 38 | 132 | 3 | (8) |
| 39 | 13211 | 5 | (9) |
| 40 | 132112 | 6 | (10) |
| 41 | 1321122112 | 10 | (21) |
| 42 | 132112211213322112 | 18 | (22) |
| 43 | 132112211213322113 | 18 | (23) |
| 44 | 132113 | 6 | (11) |
| 45 | 1321131112 | 10 | (19) |
| 46 | 13211312 | 8 | (12) |
| 47 | 1321132 | 7 | (13) |
| 48 | 13211321 | 8 | (14) |
| 49 | 132113212221 | 12 | (15) |
| 50 | 13211321222113222112 | 20 | (18) |
| 51 | 1321132122211322212221121123222112 | 34 | (16) |
| 52 | 1321132122211322212221121123222113 | 34 | (17) |
| 53 | 13211322211312113211 | 20 | (20) |
| 54 | 1321133112 | 10 | (6)(61)(29)(92) |
| 55 | 1322112 | 7 | (26) |
| 56 | 1322113 | 7 | (27) |
| 57 | 13221133112 | 11 | (25)(29)(92) |
| 58 | 1322113312211 | 13 | (25)(29)(67) |
| 59 | 132211331222113112211 | 21 | (25)(29)(85) |
| 60 | 13221133122211332 | 17 | (25)(29)(68)(61)(29)(89) |
| 61 | 22 | 2 | (61) |
| 62 | 3 | 1 | (33) |
| 63 | 3112 | 4 | (40) |
| 64 | 3112112 | 7 | (41) |
| 65 | 31121123222112 | 14 | (42) |
| 66 | 31121123222113 | 14 | (43) |
| 67 | 3112221 | 7 | (38)(39) |
| 68 | 3113 | 4 | (44) |
| 69 | 311311 | 6 | (48) |
| 70 | 31131112 | 8 | (54) |
| 71 | 3113112211 | 10 | (49) |
| 72 | 3113112211322112 | 16 | (50) |
| 73 | 3113112211322112211213322112 | 28 | (51) |
| 74 | 3113112211322112211213322113 | 28 | (52) |
| 75 | 311311222 | 9 | (47)(38) |
| 76 | 311311222112 | 12 | (47)(55) |
| 77 | 311311222113 | 12 | (47)(56) |
| 78 | 3113112221131112 | 16 | (47)(57) |
| 79 | 311311222113111221 | 18 | (47)(58) |
| 80 | 311311222113111221131221 | 24 | (47)(59) |
| 81 | 31131122211311122113222 | 23 | (47)(60) |
| 82 | 3113112221133112 | 16 | (47)(33)(61)(29)(92) |
| 83 | 311312 | 6 | (45) |
| 84 | 31132 | 5 | (46) |
| 85 | 311322113212221 | 15 | (53) |
| 86 | 311332 | 6 | (38)(29)(89) |
| 87 | 3113322112 | 10 | (38)(30) |
| 88 | 3113322113 | 10 | (38)(31) |
| 89 | 312 | 3 | (34) |
| 90 | 312211322212221121123222112 | 27 | (35) |
| 91 | 312211322212221121123222113 | 27 | (36) |
| 92 | 32112 | 5 | (37) |
定义一个向量 $\vec{v}$,向量的第 $n$ 项为当前串中第 $n$ 个元素的个数。则下一个串为:
$$
\vec{v}’=A\vec{v},\vec{v_n}=A^n\vec{v_0}
$$
其中 $A$ 为一个矩阵,如果 $(i)$ 能产生 $x$ 个 $(j)$,则第 $i$ 列第 $j$ 行为 $x$。
再定义一个向量 $\vec{u}$,其第 $i$ 项代表 $len(i)$。则
$$
L=\vec{u}\cdot\vec{v}
$$
设矩阵 $A$ 绝对值最大的特征值为 $\lambda_0$ ,
$$
\vec{v}=A^n\vec{v_0}=A^n\left(a_0\vec{w_0}+\cdots+a_k\vec{w_k}+\cdots\right)=\lambda_0^n\left(a\vec{w_0}+a_1\cdot\left(\frac{\lambda_1}{\lambda_0}\right)^n\vec{w_1}+\cdots\right)
$$
根据 Perron–Frobenius 定理,$\forall k>0,|\lambda_k|<|\lambda_0|$,故有
$$
\lim_{n\to+\infty}\left(\frac{\lambda_k}{\lambda_0}\right)^n=0,\lim_{n\to+\infty}A^n\vec{v_0}=\lambda_0^na\vec{w_0}
$$
因此 Conway 常数 $\lambda=\lambda_0$。
可得方程
$$
x^{71}-x^{69}-2x^{68}-x^{67}+2x^{66}+2x^{65}+x^{64}-x^{63}-x^{62}-x^{61}-x^{60}-x^{59}+2x^{58}+5x^{57}+3x^{56}-2x^{55}-10x^{54}-3x^{53}-2x^{52}+6x^{51}+6x^{50}+x^{49}+9x^{48}-3x^{47}-7x^{46}-8x^{45}-8x^{44}+10x^{43}+6x^{42}+8x^{41}-5x^{40}-12x^{39}+7x^{38}-7x^{37}+7x^{36}-x^{35}-3x^{34}+10x^{33}+x^{32}-6x^{31}-2x^{30}-10x^{29}-3x^{28}+2x^{27}+9x^{26}-3x^{25}+14x^{24}-8x^{23}-7x^{21}+9x^{20}+3x^{19}-4x^{18}-10x^{17}-7x^{16}+12x^{15}+7x^{14}+2x^{13}-12x^{12}-4x^{11}
-2x^{10}+5x^{9}+x^{7}-7x^{6}+7x^{5}-4x^{4}+12x^{3}-6x^{2}+3x-6=0
$$
可解得 $\lambda\approx1.3035772690342963912570991121525498$