十木的博客

Johnson-Lindenstrauss Transform

给定误差 $\varepsilon$，JL是映射 $f:\mathbb{R}^d \to \mathbb{R}^m, m=O\left(\varepsilon^{-2}\log n\right)$

使得：

$$
\forall x, y\in P, \Vert f(x) - f(y)\Vert_2\in (1\pm \varepsilon) \cdot \Vert x - y\Vert_2
$$

具体地，取 $\mathbb{R}^d$ 上随机向量 $w$，其每一维均为独立的 $N(0, 1)$，取 $g(v):=\langle v, w\rangle$

有 $E(g^2(v)) = \sum_{i}v_i^2E(w_i^2)=\Vert v\Vert_2^2$

通过多个 $g$ 拼接即可得到：

$$
f(v) := \frac{1}{\sqrt{m}}(\langle w_1, v\rangle,\langle w_2, v\rangle, \cdots, \langle w_m, v\rangle)
$$

显然 $E(\Vert f(v)\Vert_2^2) = \Vert v\Vert_2^2$

下面给出结论：

Functors

我们首先定义 fmap 函数，其功能类似于列表的 map。

其定义如下：

1
2

class Functor f where
    fmap :: (a -> b) -> f a -> f b

可以举几个例子：

列表：

1
2
3

instance Functor [] where
    -- fmap :: (a -> b) -> [a] -> [b]
    fmap = map

Maybe 类型：

1
2
3

instance Functor Maybe where
    fmap _ Nothing = Nothing
    fmap g (Just x) = Just (g x)

简单来说，fmap 就是对一个 Functor 类型的元素中的值进行操作。

题目描述

给定一个长度为 n 的序列 ，排序的轮数 k，执行如下程序：

1
2
3
4

for i from 1 to k
  for j from 1 to n – 1
    if A[j] > A[j+1]
      swap(A[j], A[j+1])

输出排序之后的序列。

$n,k\le 2\times 10^5$

题解

1

可以离散化一下。

可以发现每次排序后如果一个数之前的所有数都比他小，那么他会向后移动到下一个比他大的数。否则他会向前移动一位，并且他前面比他大的数会少一个。

因此用树状数组统计每个数前面有多少比他大的数。如果 $\ge k$，那么他只会前移 $k$ 位；否则，在他的前面没有比他大的数之后，他会移动到此时第一个比他大的数的前一位。容易知道，最后他会移动到原来 $k-1$ 轮以后最靠前的比他大的数前一位。那么可以从大到小考虑，在他开始后退以后他就成为最靠前的比以后的数大的数。

一些关于 wqs 的例题和拓展。如果题目有贪心等做法也会给出。

P2619 国家集训队Tree I

每次给白边的边权 +c 二分。

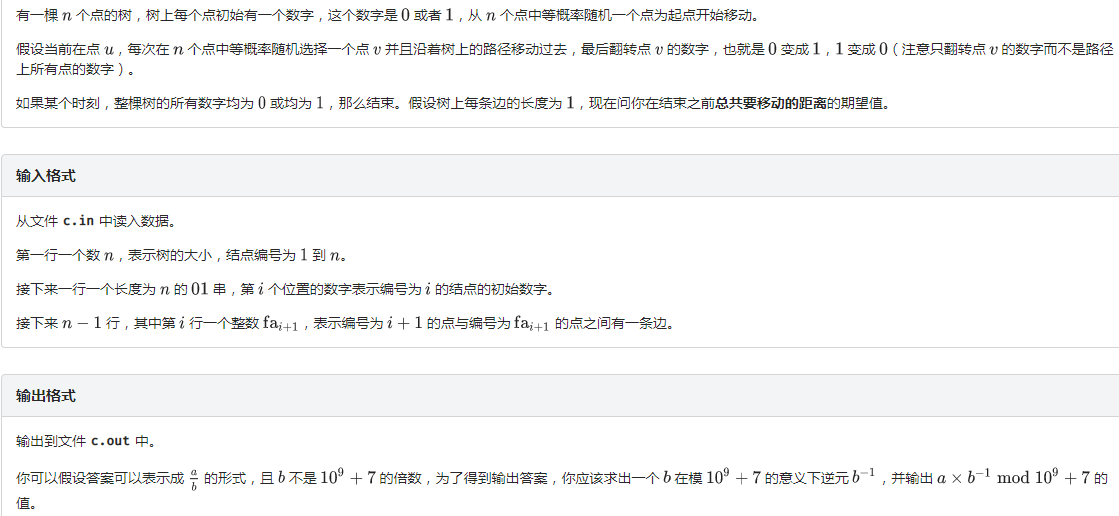
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

#include<bits/stdc++.h>
using namespace std;

void read(int &x)
{
	x=0;char c;
	while((c=getchar())<'0'||c>'9');
	while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
}

struct edge
{
	int s,t,c,_c,col;
	void ad(int cc){if(!col)_c=c+cc;}
}e[100005];
bool operator < (edge e1,edge e2){return ((e1._c==e2._c)?(e1.col<e2.col):(e1._c<e2._c));}

int fa[100005];
int root(int u)
{
	if(!fa[u])return u;
	return (fa[u]=root(fa[u]));
}
void merge(int u,int v){fa[root(u)]=root(v);}

int n,m,nd;

int chk(int x)
{
	for(int i=1;i<=m;i++)e[i].ad(x);
	sort(e+1,e+1+m);
	memset(fa,0,sizeof(fa));
	int l=n-1,i=1,ret=0;
	while(l)
	{
		while(root(e[i].s)==root(e[i].t))i++;
		ret+=e[i].col^1;
		merge(e[i].s,e[i].t);++i,--l;
	}
	return ret;
}

int binary(int l,int r,int val)
{
	int mid,tmp;
	while(l<=r)
	{
		mid=l+r>>1;
		tmp=chk(mid);
		if(tmp<nd)r=mid-1;
		else l=mid+1;
	}
	return r;
}

int main()
{
    read(n),read(m),read(nd);
    for(int i=1;i<=m;i++)read(e[i].s),read(e[i].t),e[i].s++,e[i].t++,read(e[i].c),read(e[i].col),e[i]._c=e[i].c;
    int cc=binary(-100,100,nd);
    for(int i=1;i<=m;i++)e[i].ad(cc);
	sort(e+1,e+1+m);
	memset(fa,0,sizeof(fa));
	int l=n-1,i=1,ans=0;
	while(l)
	{
		while(root(e[i].s)==root(e[i].t))i++;
		ans+=e[i]._c;
		merge(e[i].s,e[i].t);++i,--l;
	}
	ans-=cc*nd;
	printf("%d",ans);
	return 0;
}

P5633 最小度限制生成树

法 1：wqs

每次给与 s 相连的边的边权 +c 二分。判无解：求的的偏移量不在合法范围内。

法 2：贪心

约定：

• s 边：与 s 相连的边
• i 方案：选择 i 条 s 边的一种生成树方案
• i 答案：i 方案中的最优情况
• 点权：与其相连所有 s 边的最小边权
• 其他约定以括号形式给出

本文主要是对于一些算法的更为直观或感性的理解，持续更新。

本文按作者想到的时间顺序排列，与算法类别和难度无关。

Min-Max 容斥

容斥

何为容斥？容斥处理集合的交或并。自然，这可以是多个条件的与或或。

Min 与 Max 的分解

Min 和 Max 属于比较严格的限制了（严格到只有一个啊）。那么我们就分解他。

先看看 Min。Min 意味着这个数 $\le$ 所有的数。然而这样限制出来，得到的是所有 $\le$ Min 的数。不过这样形式倒是统一。

那么我们令 $f(x)$ 为 $\le x$ 的数的集合。为了方便，所有数都是正数，这样 $f^{-1}(V)=\left|V\right|$。

那么：
$$
\max(S)=\left|\bigcup_{x\in S} f(x)\right|=\sum_{T\subseteq S}\left((-1)^{\left|T\right|+1}
\left|\bigcap_{x\in T}f(x)\right|\right)=\sum_{T\subseteq S}(-1)^{\left|T\right|+1}\min(T)
$$
Min 同样。

P7514 卡牌游戏

首先，翻面的一定是左边连续一段和右边连续一段。

那么假设我都翻的右面，现在把翻的机会一个个移向左边。提前处理掉一定不会翻的卡牌，可以发现有两个区间：$[\min b_r,a_r]$ 和 $[a_l,\max b_l]$。前者用 ()，后者用 [] 表示，{} 为下一个 []，<> 是上一个。两个区间只会向左移。

答案一定是下述情况：可翻卡牌数饱和；)]}；[({)]}；<([)>]；[()] 的最小值。除最后一种情况都可直接指针扫。而最后一种情况每次事实上是维护一段最值，每次从最前删除，最后加入，可维护一单调队列。

非常笨拙然而是 $O(n)$ 的。

P7515 矩阵游戏

显然有 $n+m-1$ 个自由元，那就设在第一行和第一列。显然每一组自由元的取值唯一对应了一个矩阵。

考虑两个矩阵，他们仅有一个自由元不同。为了保证其它自由元不变，矩阵的变化一定是：在该行或列的元素应依次 $+c,-c,+c,\cdots$。

有一个例外：$a_{1,1}$。如果改变他，则所有的非自由元都会改变。为了统一我们修改第一行和第一列的所有元素。如果再对其他自由元修改使其回复原值，那么所造成的修改就是它应有的修改。

那么钦定这些自由元是 0，求出矩阵原始值。然后进行一些操作：对某一行或某一列（特殊地，第一行和第一列由同一变量控制）进行上述操作。

题目描述

Link

简意：定义字符串等级为出现在其中至少两次的最高等级的子串的等级 +1，空串等级为 0，求给定字符串的等级。

思路

首先，看到子串的问题，可以想到 SAM。然而任意子串的子串似乎还是不太好表示。在 SAM 上，我们通过边来连接前缀，用 fa 连接后缀。SAM 将子串转化为前缀和后缀。那么类似地，我们对于某一个子串，先继承它前缀的答案，然后用它的后缀，即 Parent Tree 上的祖先来更新。

在进一步的讨论之前，我们先来讨论一个问题：SAM 上一个节点表示了多个串，我们更新答案时肯定等级越大越好，所以我们存一个节点中最长子串的等级。然而这会不会影响“至少出现两次”？最长的子串没有出现两次，有没有可能有更短的子串出现两次？

我们期望它没有影响。现在来尝试证明它：

如果一个短串（非此节点中最长串）在一个串中两次出现，现在将这个短串向前拓展一位 endpos 一定不变，即任何一个位置上拓展都是可行的。那么如果这是长串的末尾，长串也一定可以拓展出去。

那么我们只需维护每一个节点上最长串的等级。

当我们计算一个节点的等级时，它一定不小于其前缀节点答案最大值。而我们再看它至少出现两次的后缀中等级的最大值，最后取最大值即可。

题目描述

P5904 POI2014 HOT-Hotels 加强版

注意代码中数据范围加大到 $10^6$

思路

这是一个乱搞算法，如果您发现错误请及时指出。

首先，可以发现三元组一定是有一个中心点，到三个点的距离相等，而且到这些点的路径只在该点重合。似乎有些抽象，放张图吧：

那么我们对于每一个节点，求一下它的子树中到它距离为 $d$ 的点。原问题中向下的那些情况就很好求了。

长链剖分，好的，这题做完了！

诶不对啊你还没求那个向上的情况呢！

向上的情况？从上往下再 DP 一次不就完了？

不对啊你求完上面的长链上的 DP 值已经没了啊！

节点的 DP 值直接从重儿子继承，相当于重儿子的 DP 值已经被覆盖了。

T1 丹钓战

水题，直接单调栈（谐音梗）。

考虑从 $[l,n]$ 转移到 $[l-1,n]$ ，注意到除了 $l$，只有在前一区间中出现在了栈顶，才有可能在新区间中出现在栈顶。维护在区间中所有出现在 $S$ 栈顶的元素，考虑 $l-1$ 对其影响：从前至后弹出不能导致 $l-1$ 弹出的元素，直到一个元素弹出了 $l-1$，此后 $l-1$ 对该区间无影响。

在计算到 $[l,n]$ 时，计算出所有 $[l,r]$，维护的是单调的位置序列，$r$ 对序列没有影响，二分 lowerbound 即可。

复杂度

$O(n\log n)$

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;

const int mxn=500005;

int n,q;
int a[mxn],b[mxn],pos[mxn],ans[mxn];
pair<pii,int> qu[mxn];
int t[mxn],l;

int read()
{
	int ret=0;char c=getchar();
	while(c>'9'||c<'0')c=getchar();
	while(c<='9'&&c>='0')ret=ret*10+c-'0',c=getchar();
	return ret;
}

int find(int L,int R,int v)
{
	int mid;
	while(L<=R)
	{
		mid=L+R>>1;
		if(t[mid]>v)R=mid-1;
		else L=mid+1;
	}
	return R;
}

int main()
{
//	freopen("stack.in","r",stdin);
//	freopen("stack.out","w",stdout);
	n=read(),q=read();
	for(int i=1;i<=n;i++)a[i]=read();for(int i=1;i<=n;i++)b[i]=read();
	for(int i=1;i<=q;i++)qu[i].first.first=-read(),qu[i].first.second=read(),qu[i].second=i;
	sort(qu+1,qu+q+1);l=n+1;
	for(int i=n,j=1,an;i&&(j<=q);i--)
	{
		while(l<=n&&b[i]>b[t[l]]&&a[t[l]]!=a[i])
		++l;
		t[--l]=i;an=l;
		for(;j<=q&&qu[j].first.first==(-i);j++)
		{
			an=find(an,n,qu[j].first.second);
			ans[qu[j].second]=an-l+1;
		}
	}
	for(int i=1;i<=q;i++)printf("%d\n",ans[i]);
	return 0;
}

T2 讨论

假设我们有一个容器，向其中一个一个加入这些集合。